¿Te cuesta entender la Química Orgánica?
¿Te cuesta entender la Química Orgánica?
Cursos de Química Orgánica para los Grados en Química, Ingeniería Química, Biotecnología y Farmacia de las Universidades españolas.
Material específico para cada Universidad con teoría, ejercicios y exámenes resueltos en vídeo, creado por Germán Fernández. Soporte para dudas por WhatsApp.
Más información en www.foroquimico.com
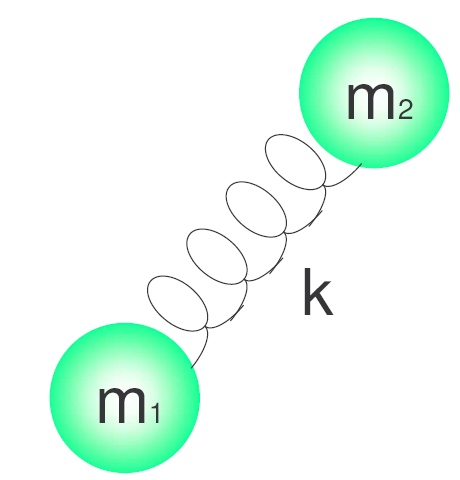
Las vibraciones moleculares pueden estudiarse con el modelo del oscilador armónico cuántico. La energía viene dada por:
\begin{equation}\label{energia-oscilador}E_v=\left(v+\frac{1}{2}\right)h\nu\end{equation}
Los distintos niveles de energía vienen dados por el número cuántico v, que toma valores 0.1.2.3.4.....
h es la constante de Planck y $\nu$ la frecuencia del oscilador que viene dada por la expresión:
\begin{equation}\nu=\frac{1}{2\pi}\sqrt{\frac{k}{\mu}}\end{equation}
Donde k es la constante de fuerza del muelle y $\mu$ la masa reducida del sistema. $\mu=\frac{m_1m_2}{m_1+m_2}$.
Dividiendo la frecuencia entre la velocidad de la luz se obtiene número de ondas $\bar{\nu}$
\begin{equation}\label{numero-ondas}\bar{\nu}=\frac{1}{2\pi c}\sqrt{\frac{k}{\mu}}\end{equation}
El estudio de la ecuación (\ref{numero-ondas}) nos permitirá predecir a qué número de ondas absorben radiación infrarroja los enlaces de una molécula. Esta ecuación sólo es aplicable a las vibraciones de tensión.
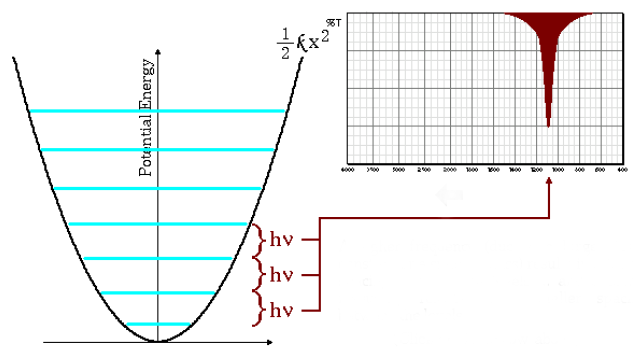
Frecuencias de absorción altas
La ecuación (\ref{numero-ondas}) indica que masas reducidas pequeñas (átomos de poca masa) y constantes de fuerza altas (enlaces fuertes) conducen a frecuencias altas. En estas condiciones las bandas de absorción salen a números de onda altos.
Como puede observarse en el gráfico las frecuencias altas dan lugar a un mayor espaciado entre los niveles energéticos.
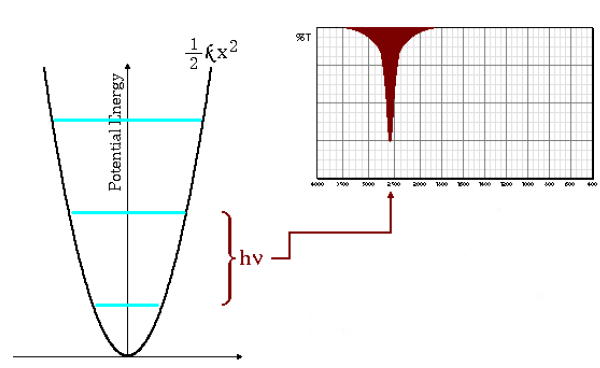
Frecuencias de absorción bajas
La ecuación (\ref{numero-ondas}) indica que masas reducidas grandes y constantes de fuerza pequeñas (enlaces débiles) conducen a frecuencias bajas. En estas condiciones las bandas de absorción salen a números de onda bajos.
Como puede observarse en el gráfico las frecuencias bajas dan lugar a un menor espaciado entre los niveles energéticos.